Now that high performance batteries are a big part of our daily lives, powering our cell phones and portable computers, we naturally want to spend less time waiting for batteries to charge up. This has prompted the search for ultrafast batteries. We would like batteries that can cycle at high currents, either discharging or charging in no time. Perhaps you’d like to charge your cell phone in under a minute, or you’d like to charge your EV in the same few minutes it takes to fill up with gasoline.
Either way, fast batteries are an engineering challenge. A good way to think of this is that it’s fairly easy to make a small battery that can cycle rapidly, but as a battery becomes larger, approaching the size it takes to power your phone or car, it gets more challenging. The way to understand this is to look at dimensional analysis.
Dimensional analysis is the engineering concept used to understand the scale or size of something, and was discovered by Galileo. Basically, to make size not matter, you have to eliminate all dimensionality in a problem. To do this you multiply/divide the important constants in the problem to make the dimensions cancel out.
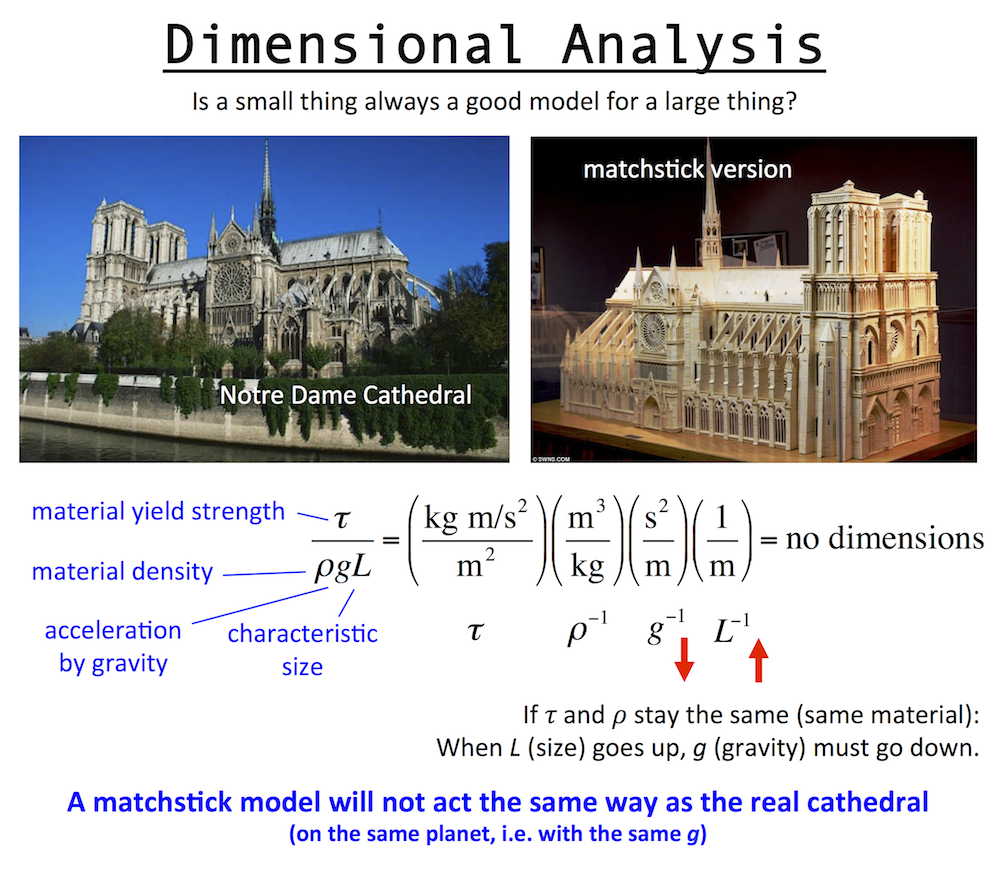
Up above is a dimensionless number for a structure, which involves: the yield strength and density of the structure materials, the gravitational constant (gravity pulls down on the structure), and the structure size, which is L, a length like the height. Consider this: is a matchstick model of Notre Dame Cathedral a fair model of the real Notre Dame cathedral? And if so, does it mean you could make the real Cathedral out of wood too?
The answer is no. The matchstick model is not at all like the real Cathedral, because while size does change between the two, gravity does not. A successful matchstick model means you could build the real Cathedral out of wood … only on a smaller planet with a lower value of g.
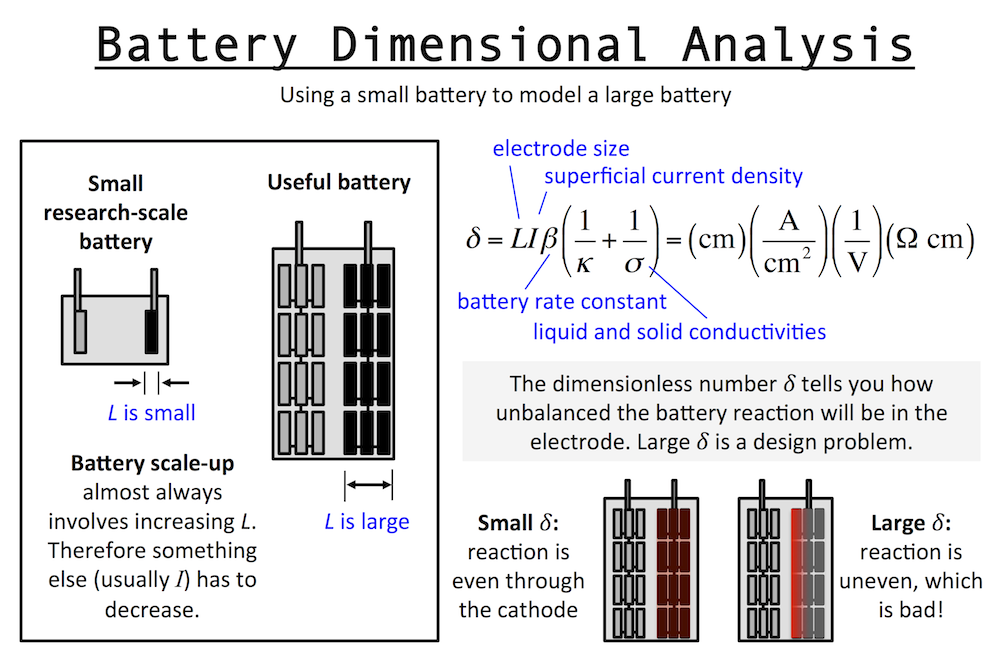
Dimensional analysis of a battery is similar to that of the Cathedral above. Imagine a small research-scale battery you might work with in a lab, and then imagine a practical battery based on it. The practical battery has been developed and scaled-up to provide the power and energy required by the application. Scaling up a battery almost always involves thickening the electrodes, and we will call this “increasing L.” The important length scale of an electrode is usually the thickness in the same dimension as current flow.
I’ve written previously about reaction rate distributions in battery electrodes (here and here). The dimensionless number δ (or John Newman’s number) tells you how balanced the reactions in a battery electrode are. When L increases, it tells you that something else has to decrease, like current I, if you want to keep δ the same. This means in general a small battery will charge fast and a large battery will charge slowly.
This is unless the other parameters in δ change accordingly to keep behavior the same … for example the porosity could be increased and that would increase the pore conductivity or κ and therefore decrease δ. But usually this goes in the opposite direction: as you scale up typically you want to achieve higher active material loading, pushing you to decrease porosity and thus decrease κ and increase δ. In fact, almost every decision you make during scale-up forces you to increase δ overall.
For this reason, the very first research decision you should try to make is to set L at the same value in your small battery that you will need in the final device. That way it becomes easier to understand scale-up, and you can extrapolate research results to real-world situations. When analyzing a fast battery, first check L and see whether scale-up will require it to increase.