Category Archives: Research

TEM of hydrated and dehydrated birnessite

Posted on by

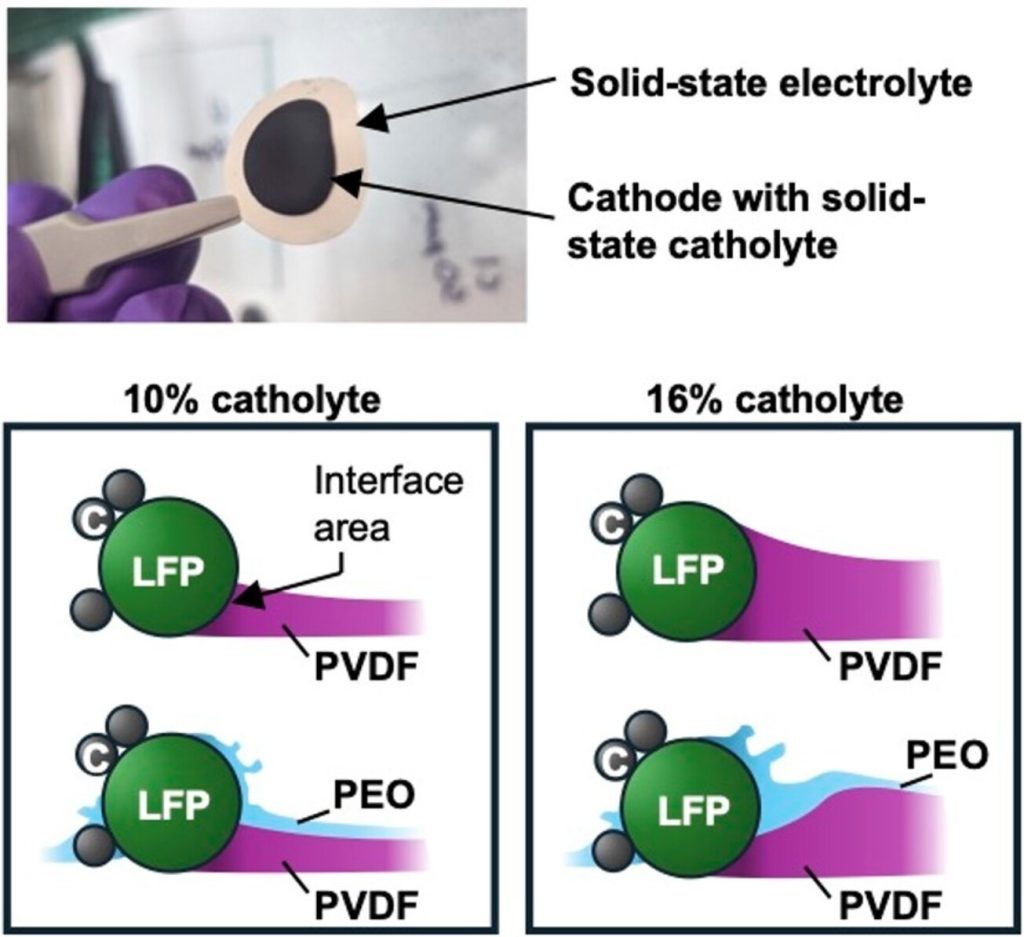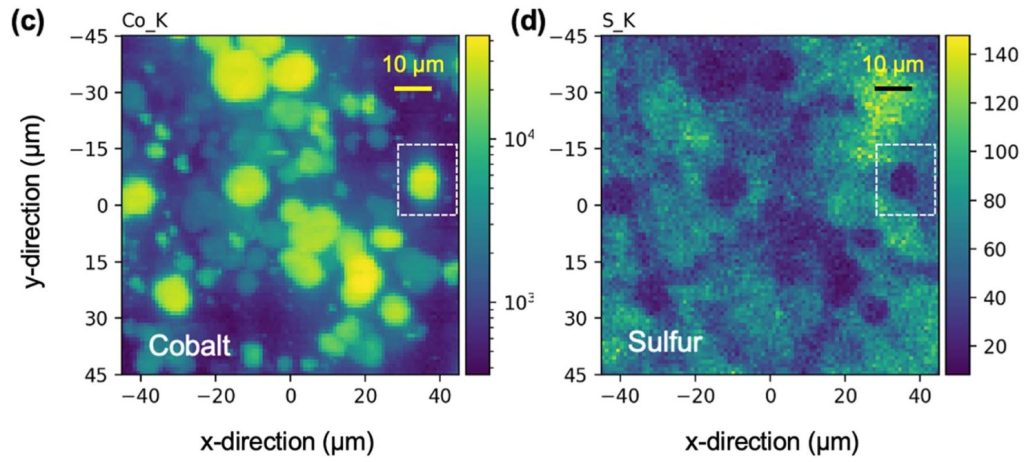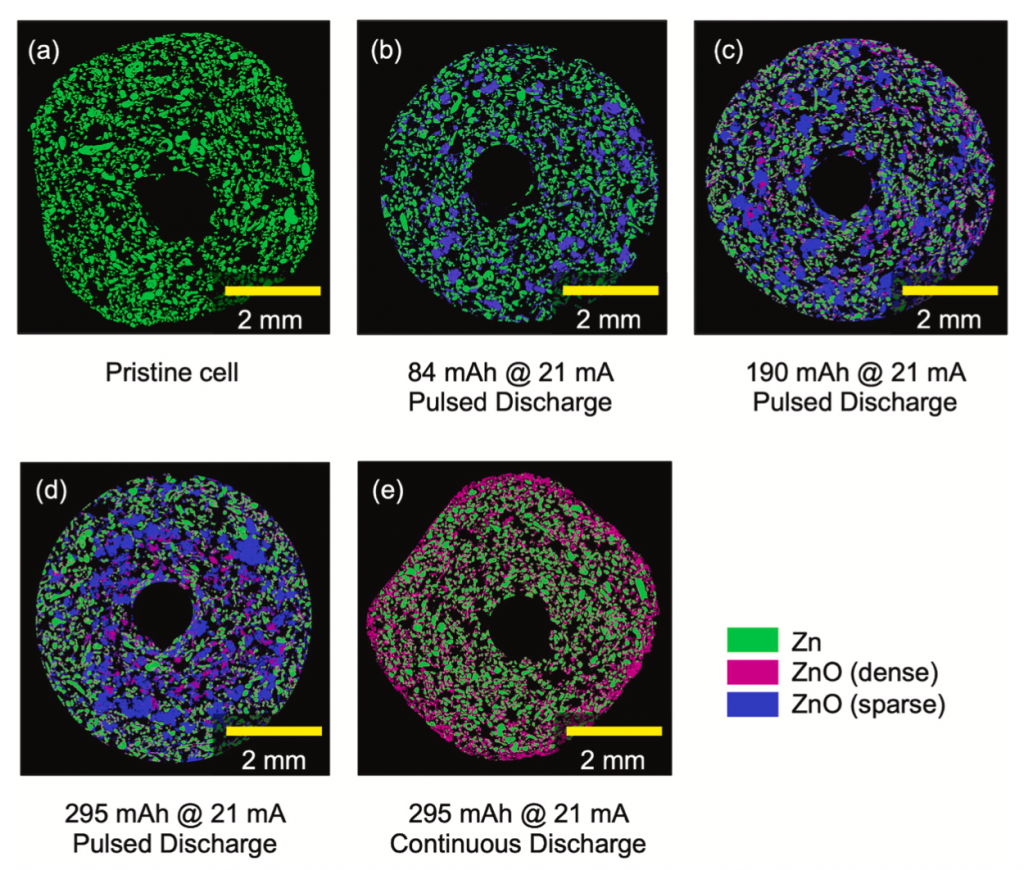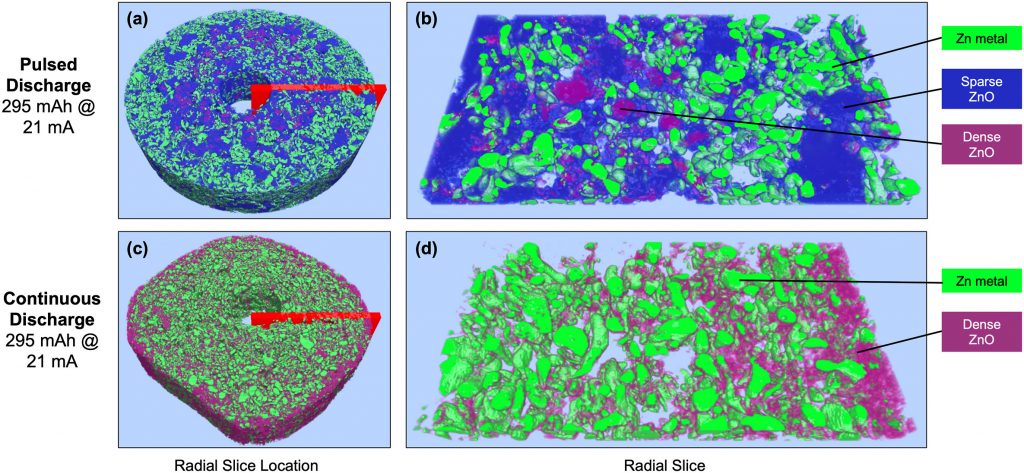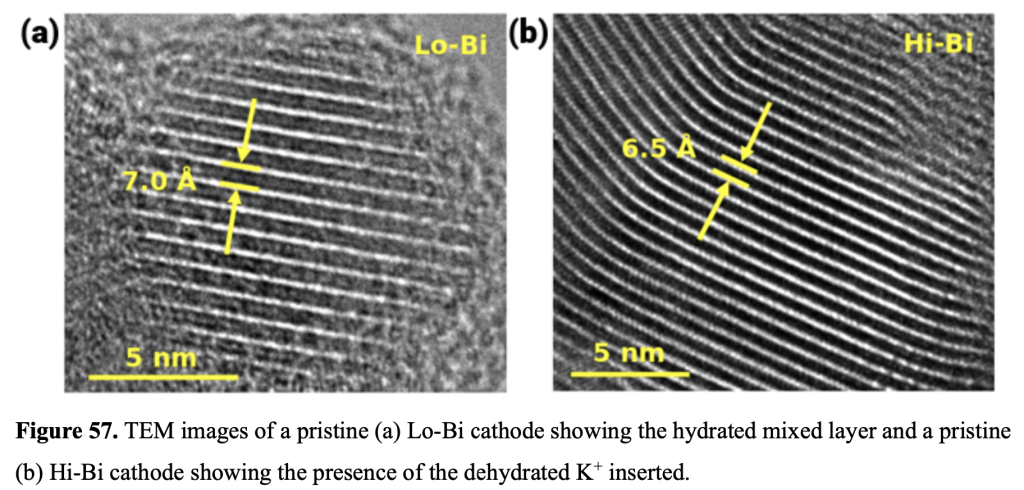
I had a reason to look at Matt Kim’s PhD dissertation, which was about synthesis of layered MnO2 birnessite compounds for Li-ion and Na-ion batteries. We published his work in this paper, but at the end of his dissertation I saw this image that didn’t make it into the paper. On the left you see a regular birnessite with a 7 angstrom interlayer, and on the right you see a dehydrated version, which is smaller because it is dehydrated and the interlayer H2O is gone.

I was looking at this and I was amazed because on the left I can see the H2O molecules between the layers. On the right you see black space only. Kind of a work of art. Matt, I’m sorry I left this out of the paper. Cutting the 60 figures down into a manuscript wasn’t the most orderly process, and I really should have left this one in. 🙂

Modeling High Current Pulsed Discharge in AA Battery Cathodes: The Effect of Localized Charging during Rest

Posted on by

New paper from us at ACS Applied Energy Materials (open access). We modeled the localized charging and discharging (i.e. balancing) that happens in a battery after a high current pulse. Great work by Dominick Guida in collaboration with Energizer.

I *wanted* this paper to be about adapting Marcus-type kinetics to MnO2 electrochemistry. But no matter what we tried, adapting a Butler-Volmer expression fit the data better. (AMH=asymmetric Marcus–Hush kinetics.)

Kinetics of sulfide-NMC batteries

Posted on by

A new paper led by Alyssa Stavola is out today. We study NMC cathodes with an argyrodite sulfide electrolyte. We find *kinetics* are ~13% of the same NMC with a liquid electrolyte, which we attribute to inactive NMC surface area.

We also use micro-XANES and XRF (shown above) to detect reduced Co2+ at the surface of the NMC. The bulk NMC is Co3+. This indicates CoS or Co3S4 at the interface.

Cylindrical alkaline batteries: Pulsed vs. continuous discharge

Posted on by

We have a new paper out in The Journal of Power Sources, which is a collaboration with Energizer. We use high energy white beam tomography to study the distribution of ZnO in the anodes of cylindrical alkaline batteries. (These are AAA, but we also studied AA sizes.) The finding is that the distribution of ZnO is a strong function of how the battery was discharged. In the image below, batteries (d) and (e) were discharged to the same depth (295 mAh) at the same rate (21 mA).

Continuous discharge (e) matched what you expect from a computational battery model: relatively dense ZnO (pink) found mostly near the separator, around the anode’s circumference. However, if the discharge was pulsed (d), the ZnO had a very low density (blue) and was mostly in large clumps in the anode interior. Since most primary batteries are used in an intermittent or pulsed manner, understanding how this affects where the resistive ZnO is located is important for getting more capacity out of the cells. We found that varying the ZnO density helps reconcile computational models with experimental results.

PhD student Dom Guida came up with a custom segmentation method to analyze these data. All the details are in the paper and the supplemental info. This tomography was special because the resolution was good (a little less than 3 microns) with a quite large field of view, letting us use unaltered AA and AAA cells and record the entire battery diameter.