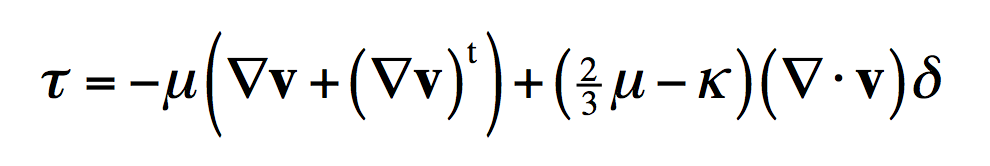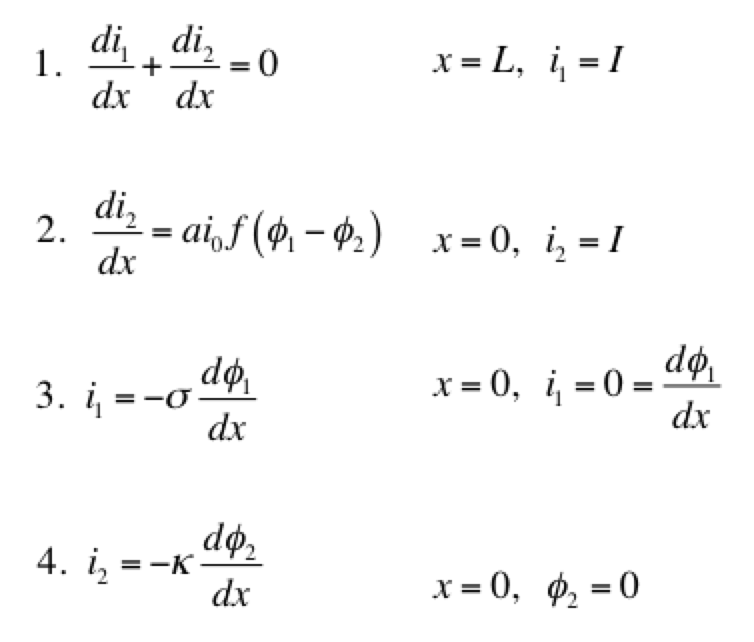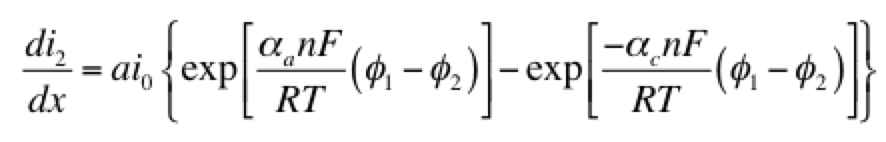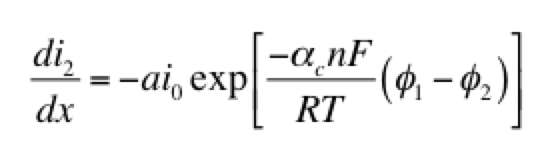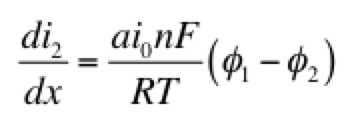A hardy thank you to the Transport Phenomena I and II class that just finished up the year at NYU. This was a great class, and sadly my last. After seven years teaching Transport in Brooklyn, I’m headed on to other things. May the no-slip boundary condition be with you!
Yesterday was the last day of class for Transport Phenomena II, ending another year of momentum, heat, and mass transport at NYU.
It’s been a busy summer, and we’ve got a few exciting battery-related surprises coming up soon at the CUNY Energy Institute. This week I’m getting ready for the start of my Transport Phenomena I class at NYU. Transport phenomena is about understanding and describing all physical changes you may find in the world.
Over the course of the year I show the class the following transport equations, which are my favorite parts of the class. Realizing these equations, which are all basically statements of the second law of thermodynamics, have a common origin is the philosophically most fun thing about studying transport.
Fourier’s law states that heat flows down a temperature gradient (with proportionality constant k, the thermal conductivity):
Fick’s law tells you mass moves from areas of high concentration to low:
Ohm’s law states that current moves down a potential gradient (and so electrons move up the gradient due to the dyslexic way current is defined):
And Newton’s law of viscosity (which is a little more complicated-looking due to the way fluids can change their density) tells you momentum transports from locations of high velocity to low.
The negative signs in these equations are the second law of thermodynamics. Those negative signs are a consequence of the fact that the universe tends towards states of higher entropy or higher probability. Of course you can make heat flow up a temperature gradient using, for example, an air conditioner. But that requires a machine, which is what you learn in a thermodynamics class. And that’s what separates “transport” from “thermo” for a chemical engineering student.
A secondary current distribution model considers:
while resistance related to concentration variations is ignored. Beginning with the equations given in Modeling porous electrodes: Part 1, the following can be written:
Eq 1 is conservation of charge; Eq 2 is some expression of electrochemical reaction kinetics; and Eqs 3 & 4 are Ohm’s law for the solid and liquid phases. The boundary conditions are such that a current density of I is being produced by the electrode. The liquid phase potential φ2 is arbitrarily set to 0 V at x = 0. The specific expression for the electrode kinetics (Eq 2) needs to be specified. The concentration-independent Butler-Volmer expression can be used:
The left hand side of this expression is the transfer current, with units of A/cm3, and gives the amount of electrochemical reaction occurring at any point. The right hand side has two components: the anodic and cathodic kinetic terms. The downside of the Butler-Volmer equation is its complexity. Finding an analytical solution to the above set of differential equations requires a more simplified kinetic expression. One possible simplification is to assume the overpotential (φ1 – φ2) is highly negative. This means only the cathodic term in the Butler-Volmer equation need be considered:
The right hand side of this expression is a form of the Tafel equation. (An analogous anodic form can be used when overpotential is highly positive.) Another possible simplification is to assume the overpotential (φ1 – φ2) is small. In this case both anodic and cathodic terms are important. Substituting the first two terms of a Taylor series for the exponentials results in:
This linear kinetic expression is valid only at low currents. Which approximation of the kinetic expression is appropriate depends on the conditions of interest. Choosing the following values for physical parameters:
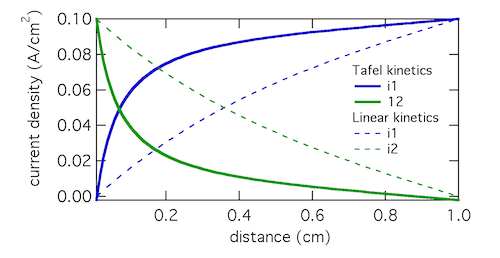
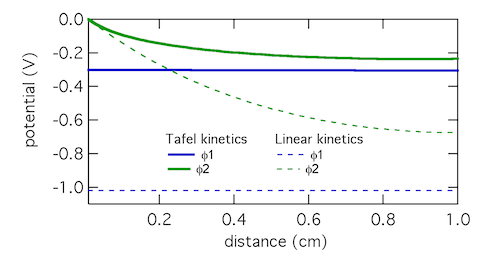
we assume that the Tafel approximation for kinetics will be valid, because the current density is much larger than the exchange current density. Solving the set of equations 1-4 for both Tafel and linear kinetics gives the results below:
The Tafel kinetic expression predicts that current exchange from liquid to solid phases (ionic current to electronic current) will be concentrated near x = 0, the location closest to the counter electrode. There (φ1 – φ2) will be near 300 mV, falling away further into the electrode. In contrast, the linear kinetic expression predicts a more even exchange of current through the electrode, and much higher values of (φ1 – φ2). This is because the linear expression is a softer function of overpotential than the exponential one. The Tafel approximation is clearly the more appropriate in this case because (φ1 – φ2) » RT/F which is 25.7 mV at room temperature.
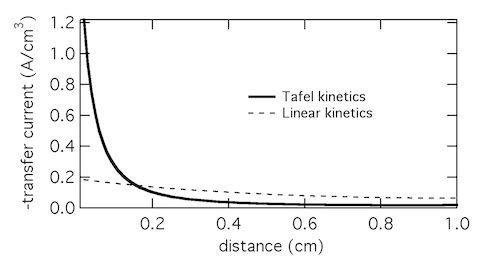
Plotting the transfer current di2/dx shows that in reality the electrochemical reaction is concentrated in the front 10% of the electrode. Linear kinetics tend to result in more uniform current distributions, but for this to be the case i0 > I will need to hold.
Click here for Modeling porous electrodes: Part 3, which is about solving porous electrode problems using Newman’s BAND method.
Nilesh Ingale got his Ph.D. yesterday here at the CUNY Energy Institute. He and I have worked closely for several years, modeling alkaline batteries, worrying about manganese dioxide. Congratulations, my man. Here’s my favorite Nilesh picture, from 2012: he’s taken Valerio’s ID to get into an event at the Electricity Storage Association conference. I don’t remember why. Maybe they had good food?