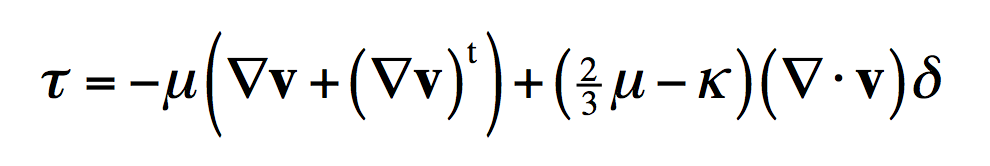It’s been a busy summer, and we’ve got a few exciting battery-related surprises coming up soon at the CUNY Energy Institute. This week I’m getting ready for the start of my Transport Phenomena I class at NYU. Transport phenomena is about understanding and describing all physical changes you may find in the world.
Over the course of the year I show the class the following transport equations, which are my favorite parts of the class. Realizing these equations, which are all basically statements of the second law of thermodynamics, have a common origin is the philosophically most fun thing about studying transport.
Fourier’s law states that heat flows down a temperature gradient (with proportionality constant k, the thermal conductivity):
Fick’s law tells you mass moves from areas of high concentration to low:
Ohm’s law states that current moves down a potential gradient (and so electrons move up the gradient due to the dyslexic way current is defined):
And Newton’s law of viscosity (which is a little more complicated-looking due to the way fluids can change their density) tells you momentum transports from locations of high velocity to low.
The negative signs in these equations are the second law of thermodynamics. Those negative signs are a consequence of the fact that the universe tends towards states of higher entropy or higher probability. Of course you can make heat flow up a temperature gradient using, for example, an air conditioner. But that requires a machine, which is what you learn in a thermodynamics class. And that’s what separates “transport” from “thermo” for a chemical engineering student.